What is a relation?
Take a deep breath: here comes some maths.
The word relationship is a common one which you think you understand. You have probably assumed - and most people do - that the name relational database comes from the fact that relationships are defined between entities. In fact this is not the case. Any kind of data model is made up of four main components: entities, attributes, relationships and constraints regardless of its type. Thus you don't need a relational database to capture relationships.
The term relation comes from a branch of mathematics called set theory which deals with groups of objects and the relationships between them. A relation is therefore a precisely defined formal construct.
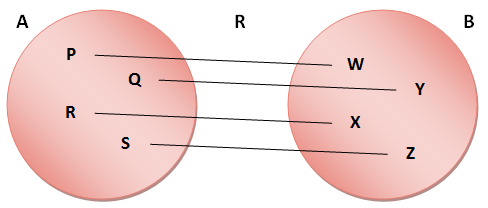
Imagine two sets, A and B, as shown below. Each one represents a group with four members
We could also represent these sets without using a diagram like this:
A ( P, Q, R, S )
B ( W, X, Y, Z )
A mathematical relation is a mapping of members of one set to members of the other set as shown in the diagram below. We can give a relation a name - the one in the diagram is called R.
In the example, each member of set A is linked to one and only one member of set B, and the relation can be expressed as a set of pairs:
R = ( (P, W), (Q, Y), (R, X), (S, Z) )
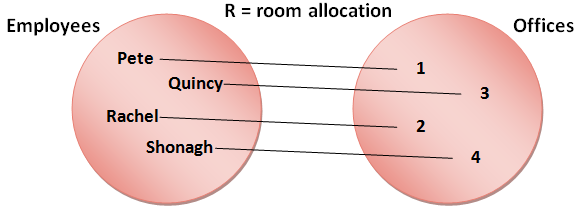
All well and good, but why is this interesting? The relevance to database structure becomes more obvious if we take some real examples rather than the traditional mathematical symbols. Let's say that set A represents the employees of a small company, and set B represents the rooms in the company's premises. Relation R now represents the allocation of people to offices.
Now the relation makes some sense:
R = ( (Pete, 1), (Quincy, 3), (Rachel, 2), (Shonagh, 4) )
We can now go one more step and represent the relation as a table rather than a list of pairs:
| employee | office |
|---|---|
| Pete | 1 |
| Quincy | 3 |
| Rachel | 2 |
| Shonagh | 4 |
Because the values in the first column all come from the set of employees, we can say that this set is the domain for this column. Likewise the set of all offices is the domain for the second column. In this trivial example, the importance of domains is not obvious; however, controlling the values that are allowed in a particular column is an important part of maintaining data integrity. The database designer therefore needs to identify a column's domain, and implement the necessary constraints to ensure that only legitimate values may be inserted. This is known as domain integrity.
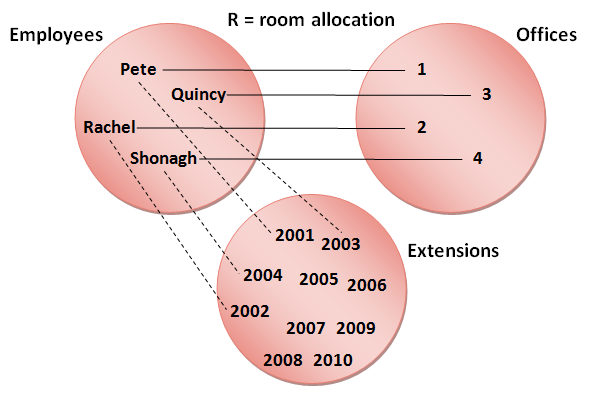
We could add another set to our example, such as the set of all telephone extensions in the company:
The relation now defines a set of triples rather than pairs - that is, each member of the relation is a group of three values, one from each set. The number of sets in a relation is known as its degree, and if we apply the same term to a database table, its degree is simply the number of columns it contains. Database tables can have many columns, and after pair, triple and quadruple, the terminology becomes awkward, so the generic term tuple is used to mean a group of related values. Sometimes, the degree is added and so you may see the expressions 4-tuple or 5-tuple, for example.
Notice in the the three-set example that not all of the values from the extensions set are used. This is an important feature of domains: they define possible values, not actual ones. the equivalent database table is shown below. Remember that a table represents an entity set, and the columns represent the attributes that each entity may have.
| employee | office | extension |
|---|---|---|
| Pete | 1 | 2001 |
| Quincy | 3 | 2003 |
| Rachel | 2 | 2002 |
| Shonagh | 4 | 2004 |
A feature of the values in a column is that they are all of the same type. This is quite a simple observation, but again there are practical consequences for relational databases. The Employee column contains the first names of people, which in computing terms are text strings. This is the datatype of the attribute. The datatype of each column is part of the definition of a table in a database, and the most basic constraint on the data stored in the table is that it must be of the appropriate datatype. Trying to store a string value in a number column, for example, would cause an error.
In this example, we have used two of the three basic datatypes used by all relational databases, strings and numbers. The third is the datatype used to store dates and times which takes different names in different database platforms. Typically, computer systems treat hours, minutes and seconds as fractions of a day, and therefore dates and times are represented in the same way.
Thinking about the datatype of an attribute and the domain of that attribute, you can see that sometimes they are the same. For example, a table containing historical events might have a description column, and an event_date column. Although we could say that only dates in the past are permitted in event_date, it is difficult to imagine what constraints to place on description values, especially when modern databases can hold strings of indefinite length. In practice though, there is usually some upper limit on the length of text string that can be stored, and this demonstrates the difference between datatype and domain: Although the datatype defines a potentially infinite set of values (think of the set of all integers), the domain of an attribute is usually a limited subset.